Does education increase intelligence and does it matter?
On Ritchie, Bates, Deary 2015; identifiability; and weak theories
How are basic cognitive skills impacted by education? Do all skills improve along a shared axis or do only very specific abilities improve? This is the question explored in Ritchie, Bates, Deary 2015 “Is education associated with improvements in general cognitive ability, or in specific skills?” [henceforth RBD]. The study is interesting for multiple reasons. It utilizes the incredible Lothian Birth Cohort, which has collected cognitive measurements for thousands of participants at Age 11 and Age ~70, enabling a unique study of test performance over the life-course. The findings are sometimes used to argue that education produces a “hollow” or “artifactual” impact on intelligence and feed the popular perception that intelligence is fixed and immutable (a claim the author disputes). It provides a useful meta-science example of the limits of model fitting and weak theories. The underlying data was made available as correlation matrices, and serves as a great hands-on introduction to structural equation modeling. Oh, and it looks like the core conclusion may be an artifact of incomplete model fitting. So let’s dive in!
The analysis
In prior work, [Ritchie et al. 2013] showed that education was associated with significantly higher IQ later in life, but no difference in reaction time tests. Here, the authors sought to characterize the broader “structure” of these associations by including more measurements and conducting formal latent variable analyses.
The basic idea is to quantify the association between the years of education participants received and their outcomes on various cognitive tests. A concern with this kind of observational analysis is the potential confounding effect of early intelligence: kids with high IQs may stay in school longer and also have higher IQ scores in old age, with education having no causal effect. To control for such confounding, scores from the Moray House Test (MHT, which has a correlation of ~0.8 with conventional IQ tests like the Stanford-Binet)1 were taken at age 11 and adjusted for in all analyses.
For the outcomes, a large battery of tests was administered to the same participants at Age 70, representing a variety of basic cognitive skills related to pattern matching and memory. Structural Equation Modeling (SEM) was then employed to extract a “general factor” (g) from the tests and evaluate the goodness of fit from three different models: (A) education is only correlated with the general factor; (B) education is correlated with the general factor and some specific skills; (C) education is not correlated with the general factor, but is only correlated with specific skills. The punchline is that Model C fit the data best, with paths from education to seven specific skills but no path to the general factor.
The authors concluded that education does not act on “general intelligence” and does not lead to “far transfer” i.e. training one skill does not improve distant/unrelated skills. A more precise interpretation (since neither general intelligence nor far transfer were rigorously defined) is that education correlates with many specific skills in a way that is different from their correlations (loadings) with the general factor (i.e. the shared variation across the skills), such that a model with direct paths to those skills provides a better explanation of the data.
If we take the general factor to be some fundamental common cause, this result might imply that education acts on individual processes directly. Of course, it could also imply that there are many underlying factors, no underlying factors (i.e. only many specific “processes” that are “sampled” by different tests), or dynamic and interactive processes leading to the accumulation of skills across individuals.
Identifiability, power, and overfitting
A good question to ask when reading any study is whether the authors are actually estimating the parameter they seek to know, and whether they have sufficiently ruled out plausible alternative models or model violations. You may be surprised how often a study proposes a parameter and then never estimates it. And it turns out that this study is one such example.
All the models we cannot identify.
Sharp-eyed readers may have caught that Model B only allows for correlations to some of the specific skills. Why not allow correlations with all skills and then directly test whether a path from Education to g improves or degrades the model fit? Because such a model is not identifiable: one can rescale the paths acting directly and the paths acting through g in an infinite number of ways while maintaining the same overall model fit. Thus, a key hypothesis — that education effects the general factor as well as all skills directly — is untestable and was not tested. The lack of identifiability for a model with all paths also means ad hoc decisions need to be made regarding which paths to add/remove from the model and in what order. Unfortunately, RBD do not provide that information2 which makes it both difficult to interpret the results and impossible to reproduce them (more on this later).
The fact that the model we are interested in is not identifiable also means it cannot be formally tested. In order to compare different models statistically, their structures need to be “nested”, meaning the parameters in one model are a subset of the other. But Model B and Model C are not nested: Model B contains parameters not in Model C (a path from Education to the general factor) and Model C also contains parameters not in Model B (paths from Education to many specific skills). Of course, one can still take two numbers and force a statistical calculator to spit out a p-value for them even if those p-values are meaningless, which appears to be what RBD did3.
All the models we do not test.
In addition to the models that are not identifiable, there are also the models that were not tested. In particular, the model where education is correlated with the general factor but early IQ is predictive of specific skills (see panel [e] in the figure below). In this model, early IQ is treated as a confounder that we want to adjust the later test measurements for (for example, if early IQ captures aspects of socioeconomic status that drive both education and later test performance)4. And that’s just within the latent variable framework outlined by RBD; there are of course many other plausible model types: models with more factors or more complex factor structures, item-level models, or models that do not estimate latent variables at all. This is a general challenge for analyses based purely on model fitting: it is rarely feasible to test (or even conceive of) every potential model.
All the models we overfit.
Another good question to ask when reading any study is: how many decisions were made before getting to the final result? If the investigators are repeatedly barreling through forks in the garden, you should start feeling a growing sense of dread. The analysis in RBD seems simple enough — just compare three models — but it hides a surprising amount of decision-making:
10 IQ tests were selected for … reasons.
The factor structure of the tests was determined using an exploratory analysis fitting multiple different structural models. A bifactor model fit the best, containing one general factor and four additional sub-factors that influence specific skills directly. A causal interpretation of this model is that skills are influenced by both a latent general factor and latent domain-specific factors.
The above model does not lend itself easily to testing a path from education, so RBD then replaced the four sub-factors with five residual covariances (i.e. paths between pairs of skills forcing them to be correlated). It is unclear how these covariances were selected (i.e. what order or stopping conditions), but this model ultimately did provide a better fit than any of the bifactor models.
One of these residual covariances (between the Age 70 MHT IQ test and the Spatial Span test) was “unexpectedly” negative, meaning that individuals who do well on the MHT tend to do poorly on the Spatial Span test (when considered jointly with the other structural constraints). The consequences and interpretation of this negative path are unclear but it was retained because it improved model fit.
As noted above, two paths between education and specific skills were selected for Model B but it is unclear how or why these paths were chosen or other paths dropped.
For Model C, three non-significant paths between education and specific skills were dropped though again the precise order and stopping conditions are not specified.
Whew! That’s a lot of fitting only to then compare the models in the same sample for the final evaluation. There’s also a catch-22 that applies more broadly to iterative SEM analyses like these: many putative factor structures are explored and one is selected, then paths for education and the Age 11 MHT are added, should the putative factor structures now all be re-evaluated and re-validated as best fitting? Then more paths are added and removed; should the factor structure again be re-validated? The implicit assumption here is that step-wise improvements to model fit will only get you to a superior model, but it is well known that such an algorithm will often converge to only a local optimum or simply overfit to noise in the sample. We shouldn’t fault RBD too much, validation in an independent dataset (or even cross-validation) just don’t seem to be common practices in this field. But it does put a damper on drawing any broadly generalizable conclusions from this analysis.
The reanalysis
The great thing about SEM is that most analyses can be run using just the matrix of measurement correlations without any individual-level data. That means you can read an interesting paper and then just copy/paste the data to experiment with it yourself. It seems like a small thing but it’s quite remarkable and worth highlighting since most fields do not have this level of reproducibility. RBD generously made their correlation matrix available, so we can now go back and re-run the path selection for Model 2, as well as test other models. I’ve also made all of the below re-analyses available in a code notebook that shows you how to do it yourself (it’s very simple stuff, I’m not patting myself on the back here), and hopefully facilitates more experimentation.
First, let’s replicate the findings using models defined by RBD. This is an important sanity check to make sure we interpreted the data correctly, loaded everything in the right order, and understood the published results. As shown in the figure below (and in code), by fitting the models described by RBD we do in fact get nearly identical path loadings, AIC differences, and chi-square differences (the absolute AIC values were substantially different presumably because RBD used individual-level data). For Model A, the loadings on g are also nearly identical to the published values. As is the headline result: Model C has the best fit. Hurray for reproducibility!
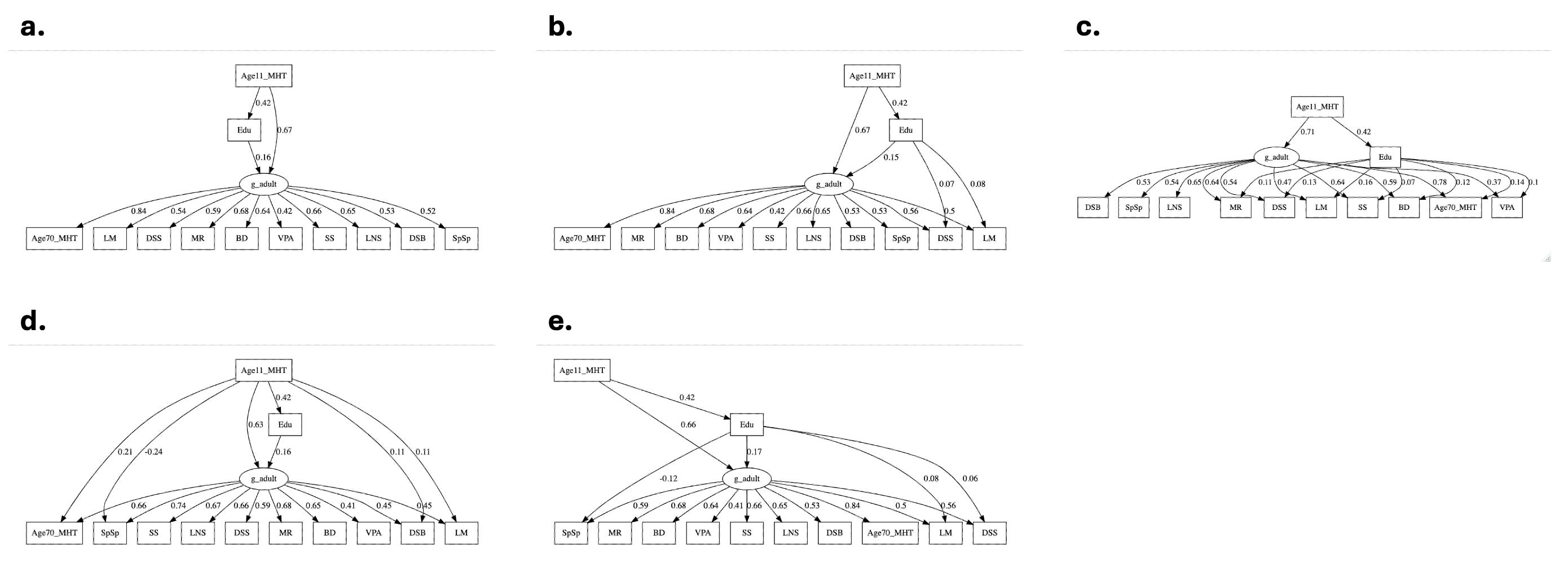
Next, while RBD did not provide the methodological details to reproduce their identification of Model B, we can do it ourselves by iterating over potential models. We’ll start with Model A and then add one path at a time from education to specific skills, retaining the path that is most significant in each iteration until no new paths improve model fit (at p<0.05) — also known as stepwise forward model selection. This approach identifies a significant (negative) path from Education to the Spatial Span specific skill in addition to the two paths identified in RBD. In fact, this path improves the overall fit of Model B to such an extent that it becomes the best fitting model! Alternative model selection approaches produced identical or nearly identical results and I could not recover the model identified by RBD. The Spatial Span path is the single most significant and should have come up first in any stepwise procedure, so either RBD dropped it for ad hoc reasons (perhaps because it was negative or because it had the lowest g-loading) or used a very different statistical approach to identifying their model. In contrast, performing the same stepwise forward model selection procedure on Model C re-identifies the same paths used by RBD. So the lack of reproducibility is exclusive to Model B and remains a mystery.
The Spatial Span test has been an odd duck in this cohort; when RBD fit the main factor models they found an unexpected negative correlation between Spatial Span and the MHT5. In the above model, it too has a negative path from education, which is counter-intuitive. What happens when we drop this test entirely, as a sensitivity analysis, and repeat the model selection procedure? The overall fit for all three models improves. Model B is still the best performing model, though both B and C become more similar to A (delta AIC of 6.76 and 1.71 respectively; down from 24.15 and 20.18 with Spatial Span). The sensitivity of the results to the exclusion of just a single test (not to mention the ad hoc choice of tests to begin with6) should perhaps further increase our skepticism of the generalizability of these results.
Finally, let’s fit the model RBD did not evaluate: where education is correlated only with the general factor but Age 11 MHT is allowed to have direct paths to the specific skills (panel [d] above and reproduced below). Remarkably, this model blows the others out of the water, with a delta AIC of >50 relative to any other model evaluated and lower error as well. Spatial Span again has a negative path from the Age 11 MHT, indicating that this unexpected negative relationship is pervasive and may be best explained by some confounding related to childhood IQ. Spatial Span also goes from being one of the least g loaded tests in Model A to the most g loaded, suggesting that the entire makeup of g may also be unstable. The fact that g is just the score that comes out of the data means we can’t know which g is the right one and simply have to trust the improved model fit.
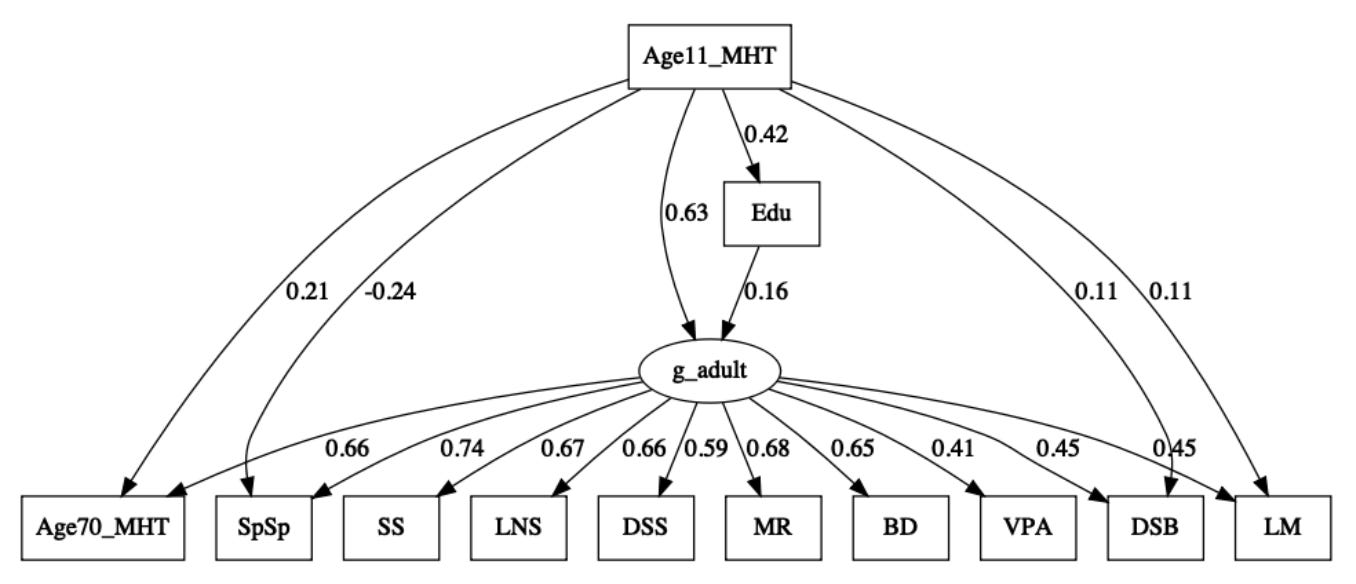
In short, proper model selection demonstrated that Model B (where Education “acts on” both g and specific skills) fit better than model C, but additional model testing revealed that a modified Model A (where Education only acts “through” g) with direct paths to individual skills was the best fit and by a wide margin. This result is essentially a complete reversal of the conclusion made by RBD: Education, in fact, has a highly significant correlation directly with the general factor, whereas it is Age 11 IQ that “acts on” (or, perhaps, confounds) specific skill scores. Should we now conclude that education does act on g?
The importance of strong theory
The authors suggest that educators might be disappointed in their finding that education does not act on g7. Now that we’ve seen, with more thorough modeling, that the effect of education directly on g actually has much more statistical support, it is tempting to simply reverse the conclusion: educators should be thrilled that schooling influences “intelligence” and “far-transfer” directly! But let us step back and ask … why all this matters? g is an unobserved variable, but if we just focus on the measured variables we already see that education is significantly correlated with 10/10 specific skills and jointly correlated with 7/10 after the shared variance is factored out. Imagine if you told someone “education does not increase intelligence, it just increases your ability on 7/10 intelligence tests”, they would surely be confused by such a claim. Then a few years later you come back and say: “Whoops, we accidentally left one path out of our model, now education does increase intelligence!”. Their confusion would be justified and, in my view, stems from the fact that g is a weak theory that encourages sloppy research.
The concept of weak theories has been articulated for decades, with [Fried 2021] as a recent example (but see also [Turkheimer 2016] on weak genetic theories or, for more vintage, [Meehl et al. 1967] on theory-testing in psychology). Fried (2021) proposed the following definition:
I define weak theories as narrative and imprecise accounts of hypotheses, vulnerable to hidden assumptions and other unknowns. They do not spell out the functional form in which two variables relate to each other, the conditions under which a hypothesized effect should occur, or the magnitude of a proposed effect. It therefore remains somewhat unclear what the theory actually explains or predicts, or how to use the theory for purposes of control (such as informing treatments in clinical psychology). Even the most simple verbal theory (e.g., “x relates to y”) can be formalized in numerous different ways …
This criticism can fairly be leveled at RBD. Their hypothesis is grossly narrative, motivated almost entirely by a quote from Spearman about education and g without ever defining what g is measuring8 , nor the functional form by which education may be expected to influence g. If g is simply a way to summarize a battery of tests, what difference does it make if education is correlated with a standard sum score versus a g-loaded sum score? And why would we interpret correlation with nearly all individual tests as evidence against far transfer?
A strong theory of g would formally define the expected relationships so that precise conclusions could be drawn from the data. It would also address many of the modeling challenges raised above. Investigators who believe in a common causal factor would be able to set the factor weights to specific theory-driven values and actually identify the models of interest and test them (imagine that!). Formal comparisons could likewise be run against models that do not assume a common cause. Decisions along the garden of forking paths would be spelled out explicitly and justified on theoretic grounds, ideally with pre-registration.
We, as readers, could also place the results in broader theoretical context: Was g measured accurately by these 10 tests? What does g measure if higher order factor models fit better or if the g loadings change substantially across models? What processes do the skills represent after g has been factored out? What is the theoretical interpretation of the covariance structure and negative covariance with Spatial Span? Why did education increase these skills but not g and is this consistent with our understanding of both? In answering these questions, one would hone in on weaknesses in the theory that could be refined or expanded. Finally, one could make formal predictions for future studies: under what other conditions should we expect education (or some other intervention) to influence g and by what form?
Instead, weak theory means g can be pretty much anything that emerges as the top factor. In this study, merely observing education-skill correlations that do not match the general factor loadings was sufficient to draw strong conclusions about the entire paradigm of education and cross-generational changes in intelligence9. It turns out the analysis may have been faulty (perhaps another area where stronger theory could have helped) and education does correlate with skills in proportion to their g loadings. But a weak theory foundation means this revised result simply floats out into the ether with no clear context or implications. Weak theories are scientific junk food: they enable bold, far-reaching claims but are actually all empty calories.
PS. Findings from other study designs
It’s tempting to end on a nihilistic note, but let us review a few more studies that have come at this question from different angles.
In the genetics literature, the findings are both simpler and more complex. The simple: IQ and g are nearly perfectly genetically correlated and have nearly identical heritability (for example, a genetic correlation of >0.9 between an extracted g factor and a simple fluid IQ test score in [Williams et al. 2023]). Whatever rescaling of subtests is done to compute g does not meaningfully change the relationship with genetic variation. Thus, the entire question of “on” g versus “on” IQ is moot.
Moreover, many genetic variants appear to influence multiple individual skills without mediation by g or influence g but have no significant effect on individual skills [de la Fuente et al. 2021]. If we treat genetics as a “natural” intervention, having an influence on g is thus neither necessary nor sufficient to have an influence on multiple skills (i.e. “transfer”). More recently, network psychometric analyses have challenged the entire premise of factor-based modeling: a network model can provide a better fit to IQ data, identify novel negative relationships, and produce substantially different estimates of twin-based heritability [Knyspel et al. 2024]. Factor models may thus not even be the most parsimonious way to summarize IQ data, let alone investigate interventions.
With respect to education and IQ, many genetic analyses have shown a bi-directional relationship between the two. Meaning that genetic variants that increase educational attainment tend to also have a consistent increasing effect on IQ and vice versa ([Davies et al. 2019] or [Anderson et al. 2020]). Such bidirectional effects are difficult to identify any uni-directional causal model without some specific manipulations. In RBD, it is likely that early education also increased the Age 11 MHT result, which in turn lead to more education in a virtuous cycle.
Finally, several studies have investigated this question by leveraging natural experiments with short-term outcomes. [Judd et al. 2021] evaluated the effect of education on a general factor by contrasting the amount of schooling a child receives (in grades 3-5, i.e. close to the age 11 measurements used as baseline in RBD) while adjusting for chronological age, socioeconomic status, and genetic scores. This design does not control for prior scores but it does enable comparisons across kids of the same age who received different exposure to education (due to the quasi-random nature of school age/enrollment cutoffs). They found a significant effect of education both on a general factor and individual IQ measurements (though a model with paths only to specific skills was not evaluated). [Bergold et al. 2017] analyzed a school reform change in Germany where schooling was shortened from nine years to eight while maintaining the same exact curriculum. Parents had no choice in enrollment, producing a natural experiment. A significant difference in the general factor was found in the group that received an extra year of schooling, up to 0.72 standard deviations, with weaker effects on specific skills. Consistent results were observed with two different IQ tests and some nice psychometric sanity checks were employed to evaluate measurement invariance (i.e. the structure of the test correlations was similar between the groups).
Thus, both in the short-term and the long-term, education appears to substantially raise IQ at the observed and latent factor level. Whereas genetics tells us there’s nothing special about g and we should probably ditch the common cause / general factor model altogether. In short: stay in school.
Acknowledgements: Thank you to RK and MN for helpful feedback and suggestions on the re-analysis. Opinions/criticisms of RBD are entirely my own.
It’s always good to look at the raw data, so here’s an example question from the MHT, which presents the test taker with a family tree and prompts them to indicate how the family members are related and what their surnames are. Readers can use their judgement on whether this is a robust evaluation of “intelligence” or may itself be confounded by cultural and socioeconomic factors.
The relevant content in the Analyses section states: “Finally, for testing the significance of individual paths within the models, we dropped them from the model (set their path weight to zero) and tested the significance of the resulting change in model fit, also using the chi-square test.”. But this is not possible since an initial saturated model with all paths cannot be identified. More details on significance thresholds and stopping conditions would have been nice too.
For example: “We then compared Model C to the previous models. It had significantly better fit than both Model A, ΔAIC = 19.08, χ2(6) = 31.08, p < .001; and Model B, ΔAIC = 9.90, χ2(4) = 17.90, p = .001.”. But, as noted, Model C is not nested in model B and cannot be compared in this way.
In a sensitivity analysis, RBD do consider an approach where IQ is first regressed out of all the specific skills and then Models 2 and 3 are compared. This showed barely any difference between Models A and C (AIC=1.77; p=0.04 even though the p-value is not valid due to comparison of non-nested models) which should probably have raised a red flag.
RBD: “we found five residual covariances that were significant in the baseline model. Four of these described clear content overlap in the tests (between Matrix Reasoning and Block Design, Logical Memory and Verbal Paired Associates, Digit-Symbol and Symbol Search, Digit Span Backwards and Letter-Number Sequencing) and one was unexpectedly negative (between the MHT and Spatial Span)”
“We focused on 10 tests” is unfortunately all the information we get in terms of how the tests were selected.
RBD: “A different result, demonstrating that education is associated with improvements in general ability, might be more encouraging to educators … Whereas education raises IQ scores, it—like the Flynn effect—does not appear to improve g.”
The closest they come is a purely data-driven definition: “the general factor universally extracted from batteries of diverse cognitive tests”
RBD: “Our findings are consistent with the notion that increased compulsory education is one of the potential mechanisms of the Flynn effect: Whereas education raises IQ scores, it—like the Flynn effect—does not appear to improve g.”




"Whereas genetics tells us there’s nothing special about g and we should probably ditch the common cause / general factor model altogether."
Crazily wrong take. Genomic SEM tells us that g is *not the only broad factor that exists*; however it also tells us that it does exist, in the sense that you've got multiple genetic variants "on g".
You have a bad habit of comparing the strength to which one thing exists against the strength to which another thing exists, and rejecting it if it doesn't vastly exceed it. E.g. you tried the same with race.
As an analogy: at work I can perform factor analysis on our performance telemetry. One of the factors I get turns out to correspond to CPU exhaustion. This isn't the only factor; there also seems to be stuff related to the database and the network. But it would be crazy for me to assert that because the CPU doesn't exhibit a much strongly statistical signal than the database, we should ditch the CPU from our models of how program performance goes.
Gracias