What happens to heritable conditions across generations?
some counterintuitive properties of the polygenic liability threshold model
When thinking about heritability we typically envision a simple continuous phenotype like height or perhaps an ordinal scale like IQ. For these traits, higher heritability very crudely implies that the trait in offspring looks more similar to the average trait in parents. But it is harder to think about the heritability of binary conditions that are either present or absent in an individual, especially when they are infrequent in the population and thus absent in most parents. Our intuitions break down and can lead to misconceptions about familial risk or how quickly a condition will be selected out of the population. Let’s look at how polygenic conditions are modeled and the implications for multi-generational patterns.
The classic monogenic / Mendelian model
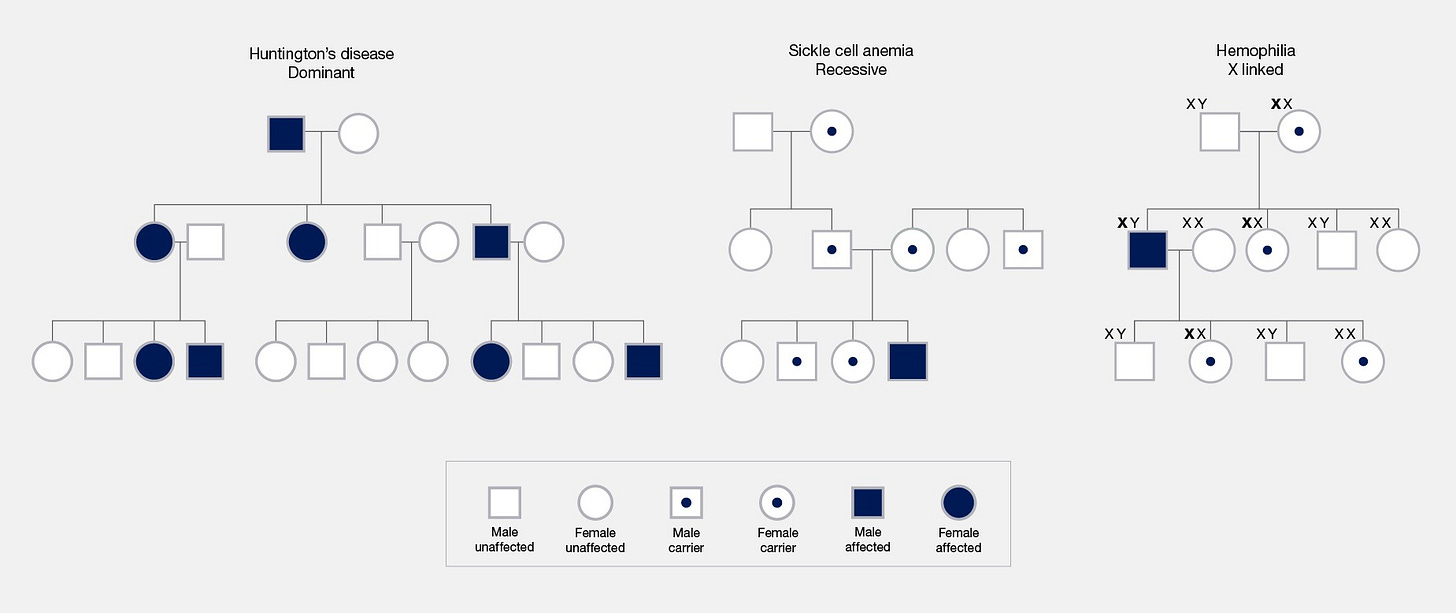
Many people are taught about heritable conditions with illustrations similar to the chart below. A genetic variant (though often referred to as a “gene”) is transmitted from parents to offspring according to Mendelian rules and the offspring develop the condition depending on the inheritance pattern: all carriers if it is dominant, homozygous carriers if it is recessive, males or homozygous females if it is x-linked, etc. All that matters is whether the offspring receive the mutation and the inheritance pattern. This model is both intuitive and memorable, and so it has shaped the way many people think about genetics. It also happens to be wrong for most common traits.
The polygenic liability threshold model
Most conditions are not Mendelian but are highly polygenic, so how do we model them? A widely used approach is to assume that the trait follows a latent/unobserved normally distributed liability and individuals are considered cases when their liability crosses a certain threshold — aka the liability threshold model (sometimes attributed to Pearson and Lee (1900) and sometimes to Wright (1934)). For a polygenic trait, the liability is driven by thousands of common genetic variants, in addition to any influences from rare variants or the environment. This model is illustrated in the schematic below from the recent paper of Huang et al. (2024), showing how affected individuals have accumulated enough influences to push them over the threshold:
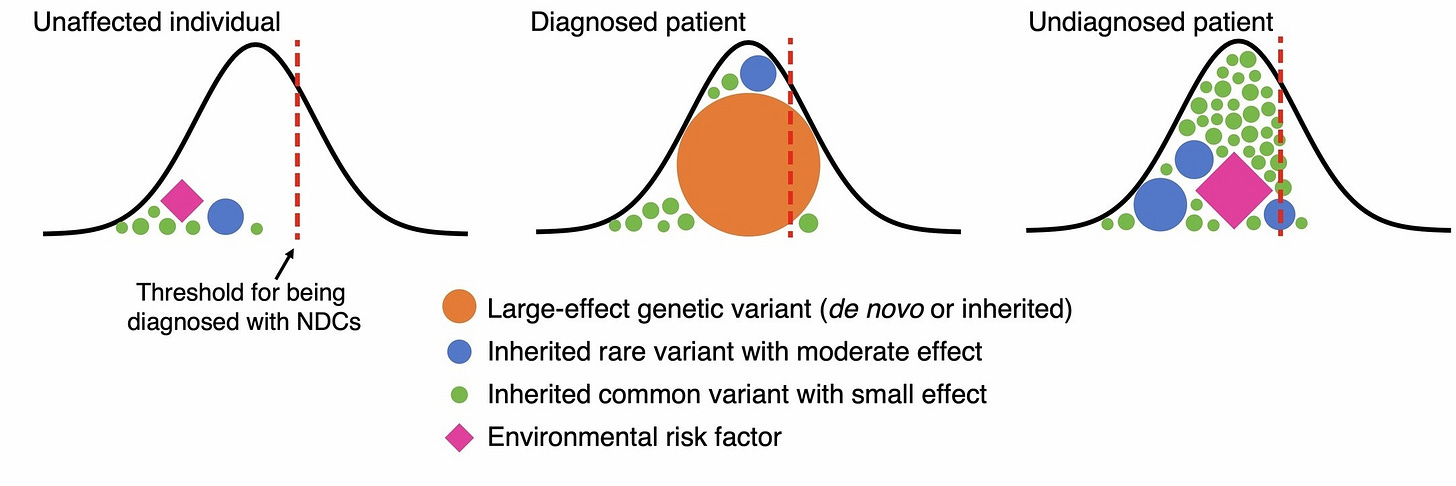
Sharp-eyed readers may also notice an interesting consequence of the model: cases with large-effect rare variants are expected to have lower polygenic/common liabilities and cases with large polygenic/common liabilities are expected to have fewer large-effect rare variants. This is a fundamental statistical property sometimes referred to as “collider bias”: if an outcome is caused by two factors that are independent in the population, then conditioning on that outcome (e.g. restricting to individuals that have a high value or are cases) can induce a negative statistical relationship between the factors in the sample. Put differently, affected individuals with a low polygenic predisposition are more likely to have needed the large-effect rare variant to push them over the threshold, creating a negative relationship between polygenic predisposition and rare variants in the cases.
A negative correlation between rare and common factors in cases has now been observed for many conditions, including in the above paper, and is often taken as evidence in support of the liability threshold model. In my opinion, such evidence is somewhat overstated and all that we can really conclude from it is that rare and common variants make some independent contributions to the observed condition. It is also good to remember that the liability threshold model is primarily preferred for its mathematical convenience and many aspects are likely to be wrong:
The threshold may actually be a spectrum: individuals just below the threshold may still exhibit mild forms of the condition, and individuals far above the threshold may have a more severe disease subtype. This is sometimes approximated as an ordinal/multi-threshold liability with “narrow” and “severe” subtypes (see: Neale 2014).
Individuals above the threshold may not immediately become cases, but rather have a much higher probability of being cases. This is sometimes modeled with an additional probability function relating the liability to the condition (see: Edwards 1969).
The underlying liability itself may not be normally distributed, which would be particularly relevant for the tails.
The model is also likely to be wrong in different ways for different traits. For cancer, it is plausible that cells have either transformed into malignant neoplasms (if above the threshold) or they have not (if below the threshold) and a hard threshold may be valid. Whereas for psychiatric conditions, there is ample evidence that individuals indeed reside along a spectrum of symptoms with a diagnostic threshold that is at least somewhat arbitrary.
Rare polygenic conditions can still be rare in affected families
With those caveats in mind, let us consider what the liability threshold model implies for the transmission of traits within families, which are not always intuitive. For example, one might naively think that a condition with 50% heritability and both parents affected would be present in offspring ~50% of the time. But this is not the case: the risk in the offspring of affected parents also depends on the liability threshold (and thus the population prevalence) because Mendelian segregation in offspring generates a substantial amount of genetic variance around their parental mean. Since many affected parents will be just above the threshold, the within-family variance in offspring will often shift them back down to unaffected status, as shown in these simulations:

Mathematically, having affected relatives can be thought of as either an increase in liability or a decrease in the threshold (see Baselmans et al. (2021) for an excellent review and visualization, or the Appendix to this post for my summary). Using these derivations and taking a 1% prevalence for the condition with 50% heritability proposed above — similar to the prevalence and inheritance patterns observed in kinship studies for bipolar disorder — we can calculate that the lifetime risk will be ~15% in offspring of two affected parents, and just ~4% in offspring of one affected parent (or sibling). These are substantial increases in risk relative to the 1% baseline, but they are still low in absolute terms and well below what one might have expected based on heritability alone. In fact, even if a 1% condition was 100% heritable, the lifetime risk in offspring of two affected parents would still not reach 100% (it would be 68%) because of the segregation variance. Just as important, the incidence in offspring with both parents unaffected is still 0.93% i.e. very close to the 1% population baseline. This is because many unaffected individuals are nevertheless at an elevated liability, and can still produce offspring with high risk due to the within-family segregation variance. In short, even for a condition with 50% heritability, most affected parents will still have unaffected offspring and most affected offspring will come from unaffected parents (if the trait is rare and follows the liability threshold model). As expected, the rates in offspring are even lower for conditions with lower heritability (estimated analytically and confirmed by simulation):

Kinship-based estimates of heritability typically assume a negligible influence of the shared environment on the trait and may be inflated if this assumption does not hold. If instead of the 50% heritability estimated in kinship studies, we use the heritability of ~20% estimated in GWAS of bipolar disorder (Mullins et al. 2021) with fewer environmental assumptions (and different genetic assumptions), the incidence of a 1% condition in offspring of two affected parents is expected to be ~4%. And if we instead use the heritability of ~10% estimated in GWAS of major depression disorder (Wray et al. 2018), the incidence in offspring of two affected parents is expected to be just ~2%. For rare traits with heritability closer to the GWAS estimate, the absolute risk even in offspring of two affected parents remains low.
Another way to think about this is in terms of the distribution of familial risk in the contemporary population of affected individuals, i.e. how likely are the cases in the current generation to have had affected parents? Just as we saw above, the majority of affected individuals are expected to be offspring of unaffected parents. Remarkably, this is true even for a condition with 100% heritability, where a full 74% of cases are still expected to come from families with unaffected parents:
The predictive value of comorbidities depends on the mechanism
A different way to identify at-risk offspring is by looking for additional comorbid or genetically correlated traits in the parents. As we saw above, if one parent is diagnosed with bipolar disorder, that tells us their offspring may be at an elevated genetic liability but with a wide distribution. If the same parent is also diagnosed with major depression (which has a genetic correlation of 0.36 with bipolar) that may be indicative of an even more elevated genetic liability. In other words, genetically correlated conditions give us an additional glimpse of the underlying liability that we otherwise do not observe.
How much of a glimpse? Let’s again simulate a 50% heritable condition that has a 1% prevalence in the population, but this time also simulate a genetically correlated condition. As we saw before, having at least one affected parent yields a lifetime risk in offspring of ~4%. And as we would expect, having one parent affected with both conditions further increases that risk to ~5% (for a genetic correlation of 0.3 — the estimate for an average pair of psychiatric conditions) or ~7% (for a genetic correlation of 0.7 — the estimate for the highest pair of psychiatric conditions: schizophrenia and bipolar).

Though the overall risk still remains low, observing genetically correlated comorbid conditions can be an indicator of slightly increased risk in offspring if both conditions have high heritability and independent environmental influences.
But what if the environmental influence is not independent? What if the secondary trait is influenced by the same environmental factors as the first: individuals that experience a trauma are then at higher risk for both conditions, for example. In this case, by including the comorbid trait as a risk criteria in parents we are actually enriching for the environmental component. And if the environmental component does not get passed down to offspring (which is the case in our simulations), this procedure can actually identify families with a lower risk in offspring than if we had used only the focal trait as the criterion. Instead of getting a second glimpse of the liability, we are actually overfitting to the parental environment and diluting the genetic risk estimate. In the simulation above, families where at least one parent has a second condition with a genetic correlation of 0.3 and a correlated environment produce offspring with a ~3% lifetime risk, compared to ~4% when just the focal condition is used. This overfitting is mitigated to some extent if the genetic correlation is higher, but it will always do worse than just using the primary trait.
In short, whether having a comorbid condition is a genetic risk factor for offspring or an environmental confounder depends on the actual mechanisms of the conditions and how they are transmitted to children. Mechanisms matter!
Polygenic diseases cannot be “bred out”
The liability threshold model also has implications for the techno-futurist (or perhaps techno-dystopian) theories about the elimination of genetic diseases through selective breeding. These views are again likely informed by intuitions around Mendelian disorders where every carrier develops the condition. Indeed, if all individuals with a monogenic dominant condition stop having offspring then no one with a risk allele will be born in the next generation, the risk will be selected out, and the heritability will immediately drop to zero. But, as we saw above, a polygenic liability behaves very differently: many affected individuals have healthy offspring and many healthy individuals have affected offspring. If affected individuals stop reproducing, the heritability does not drop to zero, but rather each of the thousands of causal alleles decrease in frequency by a very small amount1, the mean liability is slightly decreased, and the variance of the liability slightly reduced.
We can investigate this behavior in multi-generational simulations where everyone with the condition stops having children while everyone else mates randomly and produces two offspring. We will compare a polygenic/infinitesimal model where the underlying liability is perfectly normally distributed to a monogenic model where the condition is driven by a single polymorphism with 5% allele frequency (i.e. an additive binomial model). The heritability is set to a fairly high value of 50% to make the influence of genetics more apparent, and the liability threshold is tuned so that the starting prevalence is the same between the polygenic/infinitesimal model and the monogenic one (landing at a population prevalence of ~3.6% for both). Here is what happens to the liability and incidence over ten successive generations:

In the monogenic model (red), we can immediately see a second mode in the liability distribution, which corresponds to homozygous carriers of the risk allele (as an aside, this is an example of a liability that is not normally distributed). When these individuals do not produce offspring, a substantial fraction of risk allele carriers is removed from the subsequent generation, and the mode drops rapidly. After five generations — which is still a fairly long time! — the condition is at a prevalence of <1% and after ten generations it is essentially absent from the population. Even for a monogenic condition this process still takes multiple generations because the genetic mechanism is additive and the penetrance is incomplete, allowing for carriers of the risk allele that do not develop the condition.
In the polygenic model (purple) the selection in each generation shifts the underlying liability slightly towards unaffected individuals (and also slightly reduces the genetic variance). After ten generations (by which point the monogenic condition had already been effectively eliminated) the polygenic condition is still at an incidence close to 2%. As both the genetic variance and the incidence are decreasing in each generation, the per-generation impact of selection also gradually decreases. To be clear, modeling the long term response to selection in real populations is very challenging and the response to selection can often be unpredictable. But even in this contrived scenario with a large heritability, a fixed environment, and complete, persistent negative selection for many generations — even in this very simple world — the underlying condition remains common.
In short, the threshold model leads to a surprising relationship between genetic influences/heritability on the mechanisms we don’t see and the conditions we do see. Polygenicity additionally keeps a surprising amount of genetic variance in the population in response to even extreme levels of selection (e.g. everyone with the condition stops reproducing for many generations). Even shorter: complex heritable traits do not behave at all like simple Mendelian models.
Code for all simulations, analyses, and figures is available here.
Edit: Some figures were updated for clarity and representative traits were changed from schizophrenia to bipolar disorder to reflect more consistent heritability estimates in the literature.
Appendix
The following derivations are relevant for the calculations performed here and are transcribed from Baselmans et al. and cited work, with changes to the notation I thought were more readable. Under the truncated standard normal distribution, the mean liability for affected individuals in the population is:
where K is the population prevalence (i.e. the proportion of individuals above the threshold), and z is the height of the standard normal at the threshold (i.e. the density). As shown in Falconer 1965, given an affected individual, the mean liability in relatives is a simple function of the heritability (h2) and the coefficient of relationship (r)2:
For twins r=1 and the mean liability is just the product of the mean liability in affected individuals and the heritability; for sibling/parent-offspring pairs r=1/2 and so on. Intuitively, if heritability is zero, then the mean liability is also zero (i.e. equal to the population mean) regardless of the relationship and likewise if the relationship is zero. Given the population threshold (T), we can rescale the liability in relatives to the standard normal and simply adjust their threshold to compensate:
In other words, the liability threshold is effectively lower for relatives of affected individuals. Reich et al. (1975) further showed that ascertaining on affected relatives also slightly reduces the variance in the liability (in addition to shifting the mean), leading to the following adjustment:
And in the special case where both parents are affected (derived in Wray and Gottesman (2012) Appendix), the corresponding threshold is:
If heritability and population prevalence is known, these equations allow one to estimate the threshold in relatives and the corresponding lifetime risk. If heritability is not known but the lifetime risk in relatives is known (e.g. from population registries), this enables an estimate of the heritability. In all cases the contribution of the shared environment is ignored and mating is assumed to be random.
In fact, under the true theoretical infinitesimal model where the number of causal sites is infinite and each contributes an effect size of [1/∞] , the causal allele frequencies do not change at all in response to selection.
Importantly, all derivations and simulations here assume random mating. Under simple direct assortative mating heritability is effectively increased while within-family variance is effectively decreased. However, assortative mating can also occur on the environmental component of the trait (“wealthy families marry other wealthy families”) and thus have a complex influence on heritability.




Fascinating article!
Do you have links to any studies that support the validity of polygenic liability threshold models? I found a couple of studies up on Google Scholar where the authors claimed a PLT model couldn't explain the data (a paper on sex differences in autism rates, and a paper on heart disease, CVD, and Type II diabetes in Korean populations). In the pro-PLT model camp, I found a meta-study that implied that PLT model worked for the observed data for 8 psychiatric disorders.
How controversial is this model? I'm inclined to believe it, though, but I'd like to see more pro-PLT model studies to fully buy into it.
You might be interested in this study about nurture/nature debate:
https://scientificprogress.substack.com/p/nurture-not-nature