What are we learning from the genes of siblings?
Family-based genetic analyses come of age
Update: Some additional comments/responses from Alex Young, senior author on the Tan et al. study discussed here.
Two interesting papers on sibling-based genetic analyses came out this week: Tan et al. and Sidorenko et al.. Genetic studies of siblings/families offer several unique opportunities: the estimation of genetic effects on traits with many (but not all) biases controlled within families; and the estimation of broader aspects of heritability by exploiting the slight variations in sibling sharing across families. The main limitation is that collecting sibling data is hard and family-based approaches typically require even larger sample sizes than conventional analyses. To overcome the limitations, these two studies put together data from >100k siblings/families, a truly impressive feat that the authors and study participants should be commended for; conducting sophisticated analyses distributed across many cohorts is no small task. Tan et al. also made their full summary data publicly available with their pre-print, which will be immediately useful for many other research questions. So let’s start there.
Within-family GWAS
Tan et al. conducted a family GWAS analysis across 34 traits with up to ~100,000 families for some (the sample size per trait varied substantially). The basic idea is to gather genetic data from families (largely composed of siblings, who are the easiest to recruit), “impute” the genotypes of missing 1st-degree relatives, subtract out the family/parental genetic component, and then run standard genetic analysis on what is left. Removing the family component is the secret sauce that takes out a lot of biases which are otherwise difficult to control. Though, it is worth noting, the family GWAS can also introduce some biases by effectively only testing the children of heterozygous parents at each variant (see: [Veller, Przeworski, Coop, (2024)] for more1), or due to cross-sibling effects or non-random mating.
This is certainly not the first large-scale family-based genetic analysis, but it’s one of the first where the analytical approach feels fully mature and the specific parameters being probed are fairly well defined. This is also a paper chock full of interesting results and for which the senior author already wrote a detailed lay summary, so I’ll try to hit some points I thought were particularly unexpected.
And the most significantly heritable phenotype is … smoking?
You’re probably used to height coming out on top of the heritability pile, but one of the most surprising results from this analysis was an estimated SNP heritability of smoking at 0.463 (population) and 0.356 (direct). This is substantially higher than estimates of ~0.10 for ever smoking in large prior GWAS. It is even more puzzling given that the closely related Cigarettes Per Day phenotype in this very analysis had the second lowest heritability at 0.014 (s.e. 0.022; direct). “Have you ever smoked cigarettes” is not a complicated question and it is hard to imagine a sub-population or survey that would produce such an outlier in terms of strong genetic effects (while simultaneously exhibiting unusually weak effects on Cigarettes Per Day). It is tempting to think that maybe a new genetic etiology of smoking has been identified, though typically when an initial analysis seems too good to be true … it is.
Socioeconomic phenotypes have very low heritability
At the other end, some of the lowest heritability estimates came from phenotypes related to socioeconomic factors: individual income (direct h2 = 0.024 s.e. 0.032), self-rated health (0.043 s.e. 0.013), household income (0.045 s.e. 0.038), and educational attainment (0.072 s.e. 0.008). This stands in stark contrast to twin and pedigree estimates of 40-50% for income-related measurements (though extended twin studies that do not assume equal environments between twins obtain much lower estimates). Depending on how seriously you take them, these numbers could have some important consequences. If you take the twin study estimate at face value, the implication is that the genetics of economic factors are almost entirely driven by very large effect rare variation that is somehow neither captured by common variant GWAS (like this one), nor by rare burden analyses of coding regions (like the Weiner & Nadig et al. (2023) estimate of <0.5% rare burden heritability for the Townsend Deprivation Index). Many people are walking around with mystery rare variants that substantially reduce their ability to advance professionally or educationally (through mechanisms that can range from the meritocratic to the dystopian). If you take the GWAS estimates at face value, then the concerns about “genetic confounding” (where rich parents have rich kids because of a shared underlying genetic advantage) have been greatly exaggerated: essentially all of the intergenerational wealth transmission we see in families is driven by, well, the transmission of wealth (and the environments it creates).
GWAS effects often capture more confounding than signal (and this is a major problem for crude analyses of polygenic scores)
Beyond comparing the heritability estimates, it is also possible to compare the individual associations that are estimated from the population and family GWAS. This provides an estimate of how much of the variation in population GWAS effect sizes has nothing to do with the direct effect sizes observed in family GWAS (after accounting for measurement error) — which the authors refer to as “confounding”2 . Let’s start with height: about 10% of the variance in effects learned in the population GWAS is confounded. This relatively small amount may be explained by assortative mating (tall people marrying tall people), which induces correlations across genetic effects that would otherwise be independent and distorts the estimates somewhat. Similarly low amounts of noise were observed for BMI and lung function. That’s the good news.
The bad news is that a number of traits exhibited population effects with as much or more confounding than signal: household income (72% confounding), cognitive performance / IQ (65% confounding), and educational attainment (48% confounding). Yet again we see that traits like IQ and education are substantially more confounded than traits like height and BMI3. The specific sources of this noise are still unclear, but subsequent results were consistent with a substantial influence of population stratification: if your zip code is correlated with your genetics and also with your household income, that starts to look like an association between genes and income in a population GWAS.
The authors speculate — and I agree with their intuition — that this confounding may be less severe for the most significant associations. But where this noise will really get compounded is in the construction of polygenic scores, which typically aggregate thousands if not millions of individually weak associations into a single predictor. For traits like IQ and EA, those scores are likely to correlate more with stratification or other biases than actual direct genetic influence, making any causal interpretation essentially impossible. This is especially true when comparing polygenic score means across different populations, where stratification is even more pronounced in addition to the idiosyncratic differences in variant frequency and correlation. Cross-population confounding in polygenic scores has been widely appreciated by the field but difficult to formally quantify without a positive control that was free of stratification. Now we have that positive control, so anyone who is still pitching causal conclusions based on polygenic score differences is taking you for a sucker.
Mysterious direct/indirect effect correlations make heritability even more complicated
A unique aspect of the imputed family design is that not only can one estimate the direct effects in the offspring, but also the association of the non-transmitted variants in the parents. These non-transmitted coefficients (NTCs) estimate the association between alleles in parents and the phenotype in offspring specifically for alleles that were not transmitted to the offspring. NTCs will include “indirect genetic effects”, where genetic variation in parents influences their behavior (e.g. the parent goes to college) and in turn their child’s phenotype (the child is admitted to the same college as a legacy). But they may also include other sources of confounding, such as population stratification or the effect of genetic variation that becomes correlated due to assortative mating (because NTCs do not have a within-family control). Quantifying the correlation between the direct effects and the NTCs (in a manner similar to the correlation I discussed above) revealed multiple surprisingly negative relationships, most significantly for ADHD, household income, and cognitive performance / IQ. Taken at face value, these negative correlations imply that the variants that increase parental IQ also decrease offspring IQ. The authors propose some other possible explanations: siblings differentiating from each other, natural selection inducing negative correlations between alleles, or even just biased sampling/ascertainment of the study participants. I have written about these negative correlations in the context of embryo selection — you can probably imagine the implications — and they continue to be a fascinating genetic mystery. As a counterpoint, the direct effects and NTCs on height were significantly positively correlated: genetic effects on IQ continue to differ within families more than for height.
An important consequence of negative direct/NTC correlations is that we can no longer simply compare direct/population heritability estimates to get a sense of the scope confounding. For example, in a prior sibling GWAS by Howe et al. (2022), the direct and population heritability of IQ was estimated at 14% and 24% respectively and significantly different (though see the next section for a surprise) — implying substantial environmental confounding on the population estimate. In this study it was estimated at ~19% for both. Does that mean there is no environmental confounding on the population estimate in this data? Not so fast. In the presence of significantly negative NTC correlations, the population estimate can actually be deflated relative to the direct estimate, because the NTCs cancel out some of the direct effects4. And in the presence of multiple confounders, all bets are off: the population estimate can be inflated by indirect effects, population stratification, and assortative mating while simultaneously being deflated by negative NTC correlations. In short, the population-level phenotype is effectively a different trait, making heritability estimates incomparable.
Confounding operates across traits too
Moving beyond individual traits, it is also possible to estimate the genetic correlations across pairs of traits: either because one trait influences the other, or effects on the two traits are consistently pleiotropic, or some third factor influences both traits. Recently, Border et al. (2023) demonstrated that a purely environmental factor — cross-trait assortative mating (e.g. tall people marrying thin people) — can drive many of the apparent genetic correlations observed in the population. Correlations induced by assortative mating are largely eliminated in family/sibling GWAS, enabling a counter-factual estimate of the relationships one would expect to see in a randomly mating population. For most pairs of traits these two estimates were quite similar, but 22 pairs (out of 435 tested) exhibited significant differences, with 11/22 pairs involving educational attainment or IQ scores. Given the likely high-dimensional relationships across these traits (and lots of estimation error), it is difficult to draw any specific conclusions other than the fact that — yet again — population-level comparisons of EA/IQ polygenic scores should not be treated as causal (or even “biological”) and social/cultural processes distort both the phenotypic and the genetic relationships we get to observe.
Direct IQ heritability keeps dropping
Wait, what? As I mentioned, the prior family GWAS study of Howe et al. estimated a direct heritability of IQ at 14%, whereas this analysis (with somewhat distinct data and different methods) produced a direct heritability of 19%. 19% is a little bit larger than 14% and that got some people very excited. But how were these values actually estimated?
Both studies used a method called LD-Score regression (or LDSC) which can take summary-level GWAS data and estimate various interesting parameters. LDSC works by comparing the magnitude of an association to the amount of correlated genetic variation (the “LD-” or “linkage disequilibrium-” score) for each of >1 million variants across the genome: the more a variant is correlated with other variants, the higher the “LD-score”, the stronger its GWAS association should be on average (by “tagging” more effects from those correlated variants). This relationship enables LDSC to estimate some aspects of population stratification [Bulik-Sullivan et al. (2015a)], functional enrichment of heritability [Finucane et al. (2015)]5, and genetic correlation across traits [Bulik-Sullivan et al. (2015b)]. One thing LDSC was NOT intended to estimate: total heritability6. The model makes strong assumptions about the measurement of LD as well as its relationship to causal variant effect sizes, and when those assumptions are violated (as they often are) the absolute heritability estimate is no longer valid. Of course, just because a method was not intended for a task does not stop people from using it for that task, and over time it has become common to report LDSC estimates of total heritability without these caveats.
More recently, Hou et al. (2019) derived a novel estimation approach that does not make (as many) assumptions about the disease architecture and benchmarked it against LDSC. “As expected” (their words) LDSC was wildly inflated, exhibiting an upward bias for every single trait tested7. The authors also benchmarked a variant of LDSC called “Stratified LD-Score Regression” or S-LDSC, which intends to relax some of these assumptions by stratifying the heritability parameters across many genomic annotations. If variants within a certain region have an unusually LD-dependent architecture and introduce bias, putting that region into the model as a covariate can reduce some of the bias. Indeed, S-LDSC produced estimates that were much closer to the truth: with a ratio of estimated to true heritability of 1.001 on average, compared to a ratio of 1.86 for LDSC8.
So LDSC is the wrong model to use if you care about accurate heritability estimates, but this can mostly be salvaged by applying S-LDSC instead. Thankfully, all of the summary statistics from Tan et al. and Howe et al. were made available for download, and both LDSC and S-LDSC are also publicly available and easy to run. So we have all the tools we need. I’ve taken the liberty of re-estimating the heritability parameters for cognitive performance using both the old (LDSC) and new (S-LDSC) models9 and here is what we get:
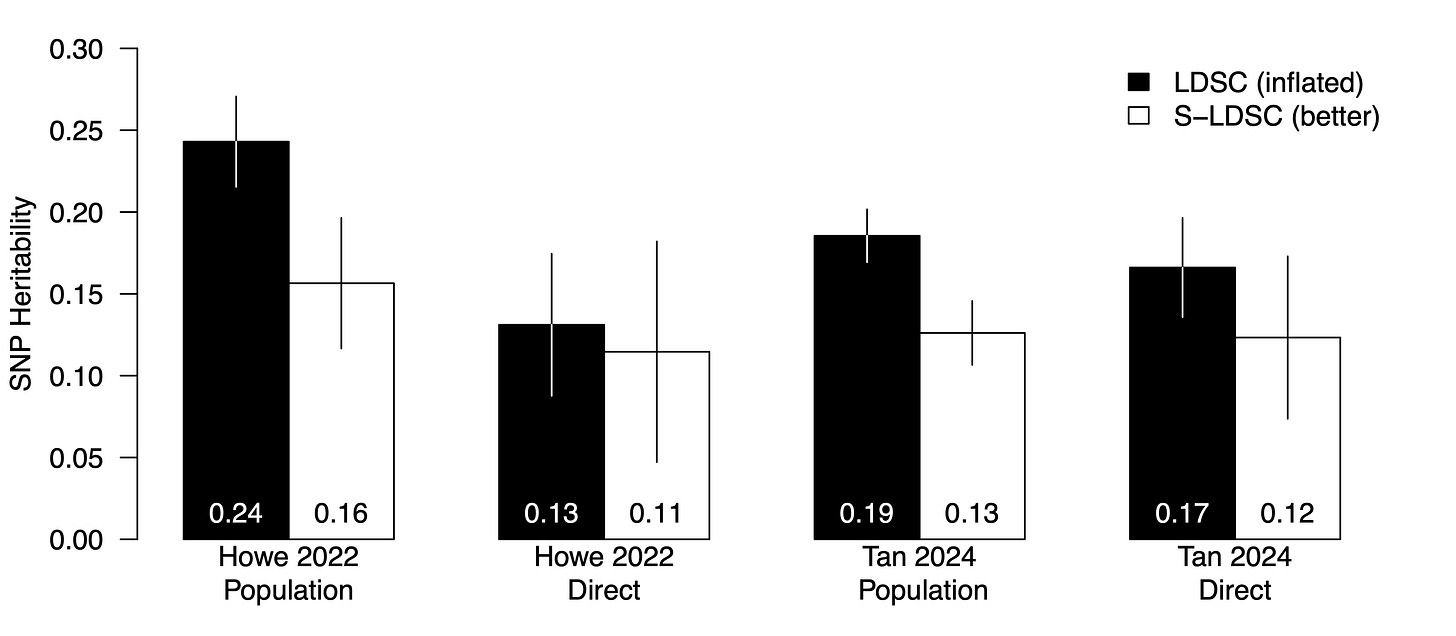
First, we can reproduce the results from Howe et al. with LDSC: a population heritability of 0.24 and a direct heritability of 0.13 (compared to the published estimates of 0.24 and 0.14, respectively). Second, when applying S-LDSC, we see a substantial decrease in both estimates: the population estimate is now 0.16 and the direct estimate is 0.11. This inflation from 0.16 to 0.24 is right in line with the average bias ratio of 1.47-1.86 observed in Hou et al. So the wrong model was used, and in hindsight it makes sense: the population estimate of 0.24 did not rely on any special within-family methodology, and yet it was one of the highest SNP heritability estimates ever reported in the literature for this trait. Next, we can roughly reproduce the results from Tan et al. with LDSC: a population heritability of 0.19 and a direct heritability of 0.17 (compared to their published estimate of ~0.19 for both). However, when we re-run with S-LDSC, both estimates drop substantially: population heritability of 0.13 and direct heritability of 0.12.
Thus the mystery of the two studies appears to be resolved. A version of LDSC that is known to produce substantial inflation was used by Howe et al. (2022)10, so Tan et al. (2024) followed suit and used the same approach. The two analyses produced idiosyncratically inflated estimates that appeared to be substantially different. When the more accurate S-LDSC model is used, the results from the two studies are much closer: 0.11-0.12 direct heritability, 0.13-0.16 population heritability. As noted above, we cannot say much about the remaining differences between direct/population estimates because of confounding from negative NTC correlations and still fairly wide standard errors. What we can say is that all the estimates are low. And as I have noted before: the more we understand these phenotypes and how to model them, the lower the heritability estimates tend to get.
And what about total heritability?
Switching gears from common variants, the second sibling-based paper this week [Sidorenko et al. (2024)] used a very large number of siblings to estimate, with some assumptions, the total heritability for height and BMI. The approach is very elegant: siblings vary slightly in the amount of genetic material they share Identical By Descent (IBD) from their parents due to the randomness of meiosis. For a heritable trait, the larger the fraction of the genome shared between two siblings, the more similar their trait is expected to be. Thus, contrasting phenotypic similarity and genetic similarity (which can be measured with genetic data) provides a way to estimate heritability in siblings without making any assumptions on which variants are causal.
This approach has several limitations, some of which have been described in the literature and some were discovered in this paper. First, because the IBD variance between siblings is low, it requires an enormous amount of sibling pairs for accurate estimation (this study collected data from a massive ~119k siblings and still had standard errors that were fairly wide). Second, if siblings influence each other or otherwise exhibit unusual environments, then this heritability estimate will be biased relative to the non-sibling population (and the bias can go in either direction). Third, the heritability estimate may include Gene-Gene (GxG) and Gene-Environment (GxE) interactions depending on the structure of the interaction, for example GxE with the shared environment will look like “heritability”. There is, so far, little evidence of GxG on these traits but substantial evidence of GxE at least on BMI (including from prior work by some of these authors in Robinson et al. (2017)). Fourth, prompted by a reviewer comment (peer review works!) the authors discover that the heritability estimate depends on assumptions about whether to quantify the sharing between siblings in terms of physical distance (i.e. proportion of genome) or genetic distance (i.e. a recombination-scaled proportion). They propose a stratified heuristic to address this, though it seems like there may be more methodological work to be done here.
Okay I’ve bored with you with the limitations, so what did they actually find? The total sibling heritability for height was 0.76 and for BMI was 0.55. This is in contrast to a common variant heritability (estimated using unrelated individuals in these cohorts) of 0.50 and 0.26 for height and BMI respectively. Even more striking, the BMI estimate of 0.55 was substantially higher than a prior estimate of 0.30 obtained using whole-genome sequencing data that directly captures rare variation. Thus there is evidence that some combination of ultra rare mutations (or other variants not captured by sequencing of either genomes or exomes), or GxG, or GxE, or cross-sibling effects can increase the variance explained by 1.5x for height and 2x for BMI relative to that of common variants. That is a lot of potential variance still out there but also a lot of potential explanations! Just for fun, we can multiply some of the direct common variant heritability estimates from Tan et al. by 2x to get a crude upper bound on the total heritability: 0.024*2 = 0.05 for individual income, 0.072*2 = 0.14 for educational attainment, 0.13*2 = 0.26 for IQ, and so on.
Next, the authors conduct a “linkage scan” to see if any specific regions are over-represented in siblings with more similar phenotypes, evidence that causal genetic variation is localized to that region. They identify just five loci for height, typically spanning many megabases, and none for BMI — owing to the low power of the linkage design for complex traits. For comparison, some of the earliest GWAS of height, at roughly half the sample size of this study, identified 50 loci. The linkage signals were, however, significantly correlated with the effects of common variants as well as with the length of each chromosome - a rough indicator that the linkage signal is sufficiently polygenic to be distributed across the genome.
How polygenic? In the introduction, the authors allude to the “omnigenic model”, which speculates that rare variants may localize in a small number of “core” genes that could be identified through linkage scans; in contrast to a “rare polygenic” architecture that would require large-scale genomic sequencing11. Some of these same authors have previously argued against the omnigenic / core gene model ([Wray et al. (2018)]), and typically a Chekhov's gun like that in the Introduction goes off in the Results. Yet their power calculations (Fig. R2) show that just 50 causal genes would be sufficient to detect a correlation with chromosome length (depending on the causal architecture), consistent with many different models. There were also some surprising relationships between common effects and the sibling heritability estimate. For example, a common polygenic score explained 38% of the variance in height in this study, but after conditioning on this score the sibling heritability dropped by just 8% (from 76% to 68%). For BMI, a polygenic score explained 9% of the variance but conditioning on it did not change the sibling heritability estimate at all. There is a lot of uncertainty in these estimates and it is unclear how exactly the sibling-regression method should behave in the context of a polygenic score covariate. But it is interesting that the heritability does not seem to budge much even when accounting for a lot of common genetic variation.
At the moment, we know essentially nothing about what these additional sources of variance are other than that we haven’t found them yet and they likely involve >50 causal elements12.
“The consequence is that if there is heterogeneity in effects between the children of homozygous and heterozygous parents, family studies will generally result in a biased estimate of the average effect of an allele in a population. In the case of the effect size estimated by a family GWAS for a single locus, the estimate can nonetheless be viewed as a LATE for the children of heterozygotes, and thus has internal validity for a well-defined subset of families.” ~ Veller, Przeworski, Coop, (2024)
Which can include some mix of population stratification, bias from assortative mating, study participation, or complex direct/indirect effect correlations.
“These results indicate that confounding factors uncorrelated with DGEs make a relatively small but non-negligible contribution to GWAS of traits such as height and BMI but comprise the majority of population effects for some phenotypes” ~ Tan et al. 2024
“A phenomenon related to deflation of population effects is negative genome-wide correlation between DGEs and average NTCs, first noted by Young et al. for cognitive performance and neuroticism in the UK Biobank. … So if DGEs and average NTCs are negatively correlated, they will tend to cancel each other out, resulting in deflated population effects” ~ Tan et al. 2024
Full disclosure: A paper I am a middle author on.
“Under strong assumptions about the effect sizes of rare variants, the slope of the LD Score regression can be re-scaled to be an estimate of the heritability explained by all SNPs used in the estimation of the LD Scores (Supplementary Table 1). Relaxing these assumptions in order to obtain a robust estimate of the heritability explained by all 1000 Genomes SNPs is a direction for further research; however, we note that the LD Score regression intercept is robust to these assumptions.” ~ Bulik-Sullivan et al. 2015a
“As expected [Bulik-Sullivan et al. 2015a], LDSC (in-sample) yields inflated estimates.” ~ Hou et al. 2019
LDSC was so inflated that the authors did not bother to quantify the amount, but one can easily derive these ratios from the values provided in Table 2. Or one can compute the slightly more stable ratio of averages: 1.47x inflated for LDSC compared to 0.96x deflated for S-LDSC.
All code and data outputs are available in a github repository with detailed instructions on how to reproduce the results. After downloading the data, the entire analysis takes only a few minutes.
To be clear, I don’t think there was any ill intent here, LDSC is faster and easier to run, and the results are easier to test for differences. It just happens to be significantly biased.
“For example, if common variation acts on phenotypes through gene expression networks that ultimately affect gene regulation at a small number of core genes [Boyle et al.], then residual genetic variation caused by rare variants may concentrate on those core genes in cis, and either large-scale, population-based, exome sequencing studies or large-scale, family-based linkage studies may identify such genes. In contrast, if residual genetic variation is just as polygenic as common genetic variance, then large-scale, population-based, whole-genome sequencing studies would be best for variant discovery.” ~ Sidorenko et al. 2024
“It is currently unknown what the genetic architecture of the remaining variants is in terms of allele frequency and effect sizes. All we can say for now is that they are not captured by common SNPs and large whole-exome sequencing studies. Future studies on WGS data and large sample sizes, for example, in the UKB, may be able to refine the genetic architecture for height and BMI and other complex traits.” ~ Sidorenko et al. 2024



I said in my recent article that as GWAS methodology improved and more and more gene variants were included, heritability estimates across the board ought to go up. This was the guess of someone who has no formal education in genetics. But what you seem to be saying is that, at least for mental traits like IQ, the higher-quality the GWAS, the lower the heritability found. So do you disagree with me? Do you think the ultimate conclusion of GWAS will be that IQ has a heritability of less than 20%? My article: https://open.substack.com/pub/eclecticinquiries/p/twin-studies-exaggerate-iq-heritability?r=4952v2&utm_campaign=post&utm_medium=web
Great article!